Umbrella sampling for cosmology
This project uses umbrella sampling (US) on a cosmology model to sample extremely low-probability areas of the posterior distribution that may be required in statistical analyses of data. The technique is tested on deriving cosmological constraints using the supernova type Ia data. We show that US can sample the posterior \(\pi(x)\) accurately down to the \(\approx15\sigma\) credible region in the \(\Omega_m-\Omega_\Lambda\) plane, while for the same computational effort the affine-invariant MCMC sampling implemented in the popular emcee code samples the posterior reliably only to \(\approx3\sigma\).
In the US algorithm, sampling of the posterior is split (or stratified) into several easier sampling problems (see the Figure below). Specifically, a sequence of overlapping window functions, or umbrellas \(\psi_i(x)\), is introduced and the algorithm samples the corresponding distributions, \(\pi_i(x)\propto \psi_i(\theta)\pi(x)\). Selecting windows in low-probability regions of the posterior and thereby confining samples of \(\pi_i\) to these regions, allows one to get a much more efficient coverage of outlying areas of the posterior and ensure discovery of widely separated peaks in multimodal distributions. In this sense, the US approach is a part of a large class of MCMC methods that are designed to sample the parameter space more uniformly, such as parallel tempering and parallel MCMC.
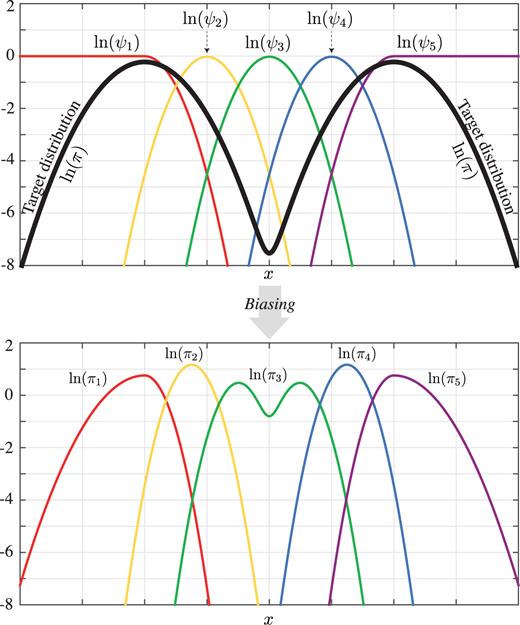
Clearly, the approach is most effective when we have some knowledge about the low-probability regions of the target distribution, as umbrellas can be designed specifically to sample these regions efficiently. Such information is often available either from prior intuition about the overall problem or from exploratory MCMC runs. We may use a collective variable (CV) to bias the simulation in a specific direction.
However US can be efficiently applied even in cases when no such prior information is available. In this case umbrella windows can be chosen so that the \(\pi_i\) correspond to tempered distributions, defined as in the Parallel Tempering method. US provides a mechanism by which samples from the high-temperature distributions (in low-probability regions) can be incorporated into more accurate estimates of tail probabilities.
To illustrate the power of the US algorithm to accurately sample the tails of the marginal posterior distribution, we use cosmological constraints derived from type Ia supernovae observations. Specifically, we sample the marginal posterior of the mean dimensionless matter and vacuum energy densities, \(\Omega_m\) \(\Omega_\Lambda\), using the SDSS-II/SNLS3 Joint Light-curve Analysis (JLA) supernovae data set and the associated JLA v3 likelihood.
Type Ia supernovae are one of the key probes of the cosmological parameters governing expansion of the Universe and played the main role in the discovery of the accelerating expansion of the Universe. The current supernovae samples, such as the JLA data set, cover a wide range of redshifts and provide complimentary constraints to those derived from the Cosmic Microwave Background and the Baryonic Acoustic Oscillations measurements.
We test two different parameterizations of windows in the US approach: temperature stratification only and a combination of the temperature stratification with a CV. The latter is possible in this case because we are interested in estimating the probability that the Universe is not accelerating, and we can define the CV in the direction perpendicular to the line separating accelerating and non-accelerating universes: \(\Omega_m/2−\Omega_\Lambda=0\).
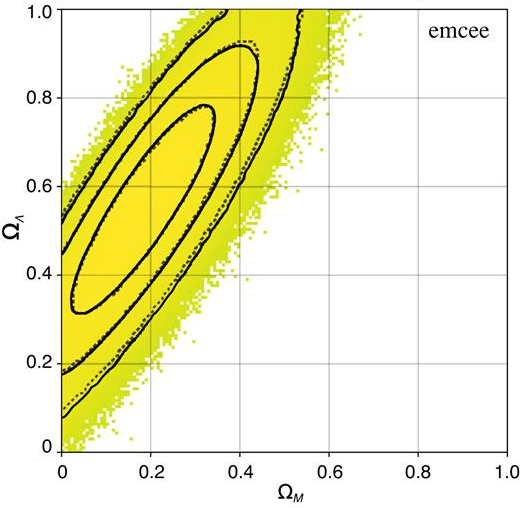
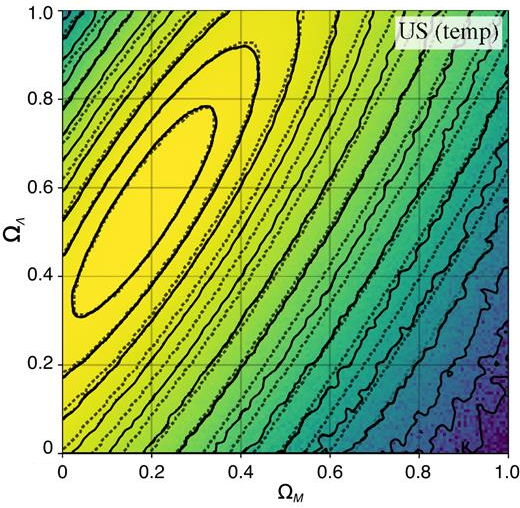
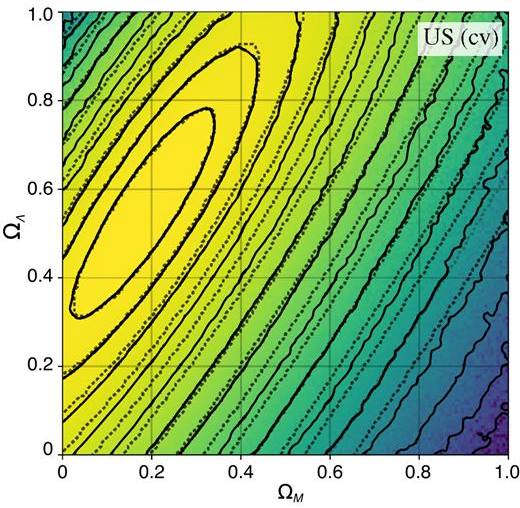
The Figure shows results of sampling the JLA v3 likelihood in six-dimensional parameter space using the Goodman & Weare algorithm implemented in the emcee package, and US with different choices of the umbrella partition. Here, we sample the JLA v3 likelihood using the COSMOSIS package to which we have added the US sampler. In each case, the sampling was done using the same number of likelihood evaluations and same computer wall time.
The runs using emcee used all 32 available cores in parallel. The US runs used 16 windows sampled in parallel, each with two cores that also worked in parallel. This gave the US results the same parallel efficiency as the emcee sampler. An MPI pool object was used to na"ively distribute the tasks evenly, without any load balancing.
The results obtained using US with only temperature show a higher variance than results using CVs, as is evident from the spikier and less-defined contours at the furthest sigma levels. This is simply because umbrella windows with the CV stratified, ensure that a fixed number of walkers sample the low-probability areas of the posterior in the plane, while in the temperature windows walkers explore the entirety of the parameter space without any restraints.
The faint dotted lines correspond to the contours assuming a Gaussian approximation of the posterior. The sampled log-likelihood surface was fit to a quadratic form using the Matlab fit function, and its corresponding sigma levels plotted. Although the initial agreement up to the third contour is good, it is clear that the Gaussian approximation fails to accurately describe the tails of the posterior. The sampled surface obtained from US shows that there exists a much ‘fatter’ tail compared to the Gaussian.