NOGIN

The NOisy Gradient INtegrator ~ A sampling scheme for high-dimensional problems with stochastic gradients

A commonly encountered problem in data science and machine learning applications is the sampling of parameters \(\theta \in \mathbb{R}^D\) from a product distribution over a dataset \(y\) containing \(N\) observations \(y_i\). Combined with a regularizing prior distribution \(\pi_0(\theta)\), the aim is to generate points distributed according to the target distribution \(\pi(\theta)\) where

\[\pi(\theta) \propto \pi_0(\theta) \prod_y \pi(y_i | \theta).\]

Such a formulation is commonplace in (e.g.) Bayesian inverse applications, where \(\pi(\theta)\) is referred to as the target posterior distribution. We often make moves in space using the gradient of the log-posterior (known as the force)

\[F(\theta) := \nabla \log \pi_0(\theta) + \sum_{i=1}^N \log\pi(y_i|\theta),\]

but this can be expensive if the number of datapoints \(N\) is very large. Only evaluating the force over a subset (or a batch) of data can make for a considerable efficiency saving, but we must balance the cost of the error introduced from not correctly computing the total gradient.

In this project, we assume we have some stochastic gradient \(\widetilde{F}(\theta)\) with the property that the gradient is normally distributed where

\[\widetilde{F}(\theta) \sim N(F(\theta),\,\Sigma(\theta))\]

for some positive semi-definite matrix \(\Sigma(\theta)\). Assuming we can obtain the covariance \(\Sigma(\theta)\), or some low-rank approximation to it, we can damp the additional noise introduced by the stochastic gradient and recover high-order sampling. We give the proposed algorithm below.

The Noisy Gradient Integrator (NOGIN) algorithm.

This algorithm accurately integrates the Ornstein-Uhlenbeck process with the additional gradient force. This means that in the case of a true-Gaussian stochastic gradient, and where the log posterior is quadratic, the NOGIN scheme gives no error at all! This is an especially nice property as it has been shown that in the limit of a large amount of data, posteriors approach a Gaussian distribution.

We demonstrate the power of the scheme by comparing the results against five other schemes (see the article for details). We look at the errors in the computed parameter variances as a function of the number of full passes through the dataset (epochs). We compare the results from using different batch sizes (the batch size is fixed for each run) to demonstrate the gain in efficiency.

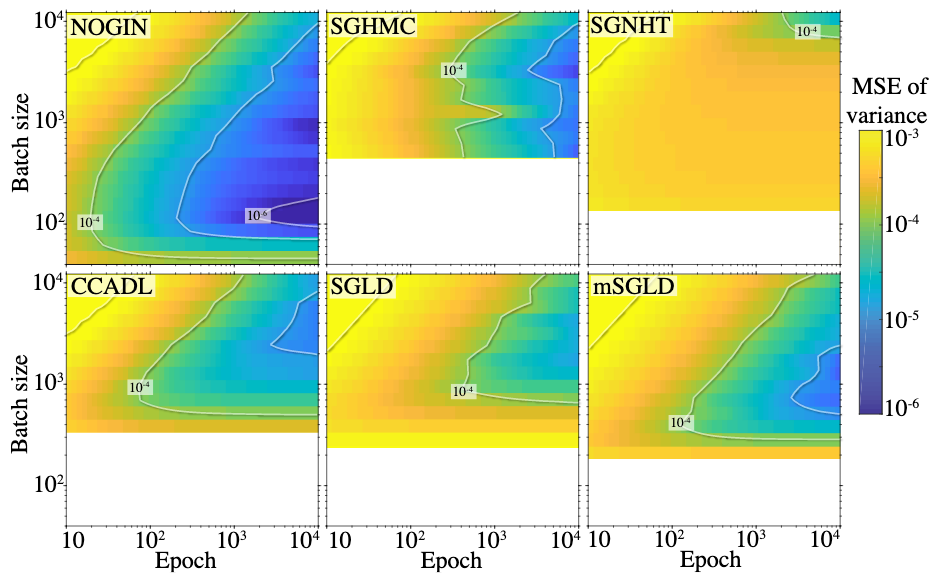
The results comparing NOGIN to five other state of the art schemes on a Bayesian Logistic Regression problem for the MNIST dataset with 12214 total datapoints. The error is shown as a function of simulation time (epoch) and the batch size, with blue indicating a low error.

The results show the optimum choice is to use around \(1\%\) data per batch, with a significant improvement coming from the NOGIN scheme.

Check out the code and the article for more information. Also take a look at another stochastic gradient scheme I have worked on, called RACECAR.